Why are Randomized Experiments the Gold Standard in Causal Inference?
Understanding the identifying assumptions in experiments.
By Murat Unal in Causal Inference
March 6, 2023
Causal inference without assumptions is impossible. Every available method requires untestable assumptions to establish causality from observed associations in the data. As such, stating the identifying assumptions and defending them is the most critical aspect of causal inference, yet it is also the most neglected one.
In my previous article we kicked off the discussion around this topic by describing what identification is and why it takes precedence over estimation in causal inference. As a reminder, identification, essentially consists of clearly stating the assumptions required for statistical estimates obtained from the data to be given a causal interpretation as well as advocating for them in our causal analysis. In what follows we discuss identification in randomized experiments a.k.a. the gold standard among all the identification strategies in causal inference.
What gives experiments a special status among other identification strategies? It is two things. First, well-conducted experiments require the minimum set of identifying assumptions to establish causality. Second, these assumptions are much more plausible than those required by other methods. The combination of these two facts increase the credibility of the causal inference in randomized experiment.
To aid in discussion, let’s again consider a simple case with two treatment conditions described by a binary random variable, \(T_i=[0,1]\), and denoting the outcome by Yi. We are interested in finding the average treatment effect (ATE), which is the difference between the expected values:
\[\tau = E[Y_{i1}] - E[Y_{i0}]\]
where \(Y_{i1}\) denote the potential outcome for subject \(i\) if they are treated and \(Y_{i0}\) denote the potential outcome for subject \(i\) if they are not. If it is not clear what potential outcomes means, I highly suggest you read the article linked above. You will see a concrete example and it will help you follow the rest of this article.
Because we only have access to a sample from the population, we only observe the conditional expectations \(E[Y_i|T_i=1]\) and \(E[Y_i|T_i=0]\), which are the expected outcomes among the treated and the control, respectively, we see in our data. Now, to claim what we obtain by taking the differences of the conditional expectations is the ATE, our causal estimand, we need to show they are equivalent to the unconditional expectations. The way to do this is by making assumptions and convincing our audience about their plausibility in our specific context.
Identification Part 1: Stating the Assumptions
In randomized experiments the identifying assumptions are the following:
Independence: the potential outcomes are independent from treatment status.
SUTVA (Stable Unit Treatment Value Assumption): (1) No interaction effects, meaning treatments received by one unit do not affect outcomes for another unit. (2) No hidden variations of treatment, only the level of the treatment applied to the specific subject potentially affects outcomes for that subject.
Technically, in addition to the two identifying assumptions, we also assume no systematic attrition among experiment subjects and absence of noncompliance.
With these assumptions we can write the expectations of the observed outcomes as follows:
\[\begin{align*} E[Y_i|T_i=1] &= E[Y_{i1}T_i + Y_{i0}(1-T_i)|T_i=1]] = E[Y_{i1}|T_i=1] = E[Y_{i1}]\\ E[Y_i|T_i=0] &= E[Y_{i1}T_i + Y_{i0}(1-T_i)|T_i=0]] = E[Y_{i1}|T_i=0] = E[Y_{i0}] \end{align*}\]
This allows us to use the outcomes of the treated and control in our data to obtain the ATE:
\[\tau = E[Y_{i1}] - E[Y_{i0}] = E[Y_i | T_i = 1] - E[Y_i | T_i = 0]\]
Another way to see these assumptions in action is to look at the following decomposition:
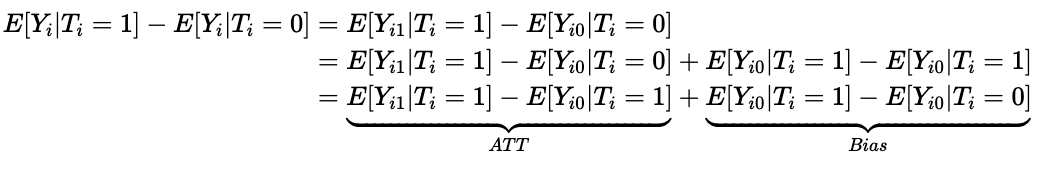
The independence assumption effectively eliminates the Bias term and we are left with the ATT (average treatment effect on the treated), which amounts to the ATE.
Identification Part 2: Defending the Assumptions
A direct consequence of this identification strategy is that it allows us to assert that the treated and control groups will be identical in all aspects, observable and unobservable, except for the differences in treatment assignments.
Moreover, if we have a well-conducted experiment with no systematic attrition among subjects then convincing our audience about the validity of the identifying assumptions will be much easier.
To make things concrete, let’s describe the relationship between the outcomes, \(Y_i\), the treatment \(T_i\), and covariates \(X_i\) using a model and for simplicity let’s assume it is linear:
\[Y_i = \beta_iT_i + \alpha_1X_{i1} + \alpha_2X_{i2} + \cdots + \alpha_PX_{iP} \]
The \(P\) covariates, which may be very large, include observed or unobserved other linear effects on the outcome and \(\beta_i\) is the individual treatment effect, which is the difference between the two potential outcomes, \(Y_{i1}-Y_{i0}\). We don’t observe this effect, but subtracting the average outcomes among the controls from the average outcomes among the treatments gives us this:
\[\bar{Y_1} - \bar{Y_0} = \bar{\beta} + \alpha_1(\bar{X}_{11} -\bar{X}_{01}) + \alpha_2(\bar{X}_{12} -\bar{X}_{02})+ \cdots + \alpha_P(\bar{X}_{1P} -\bar{X}_{0P})\]
which shows that we get what we want through the difference in means when the means of all the other effects on the outcomes are identical in the two groups.
This is the case of perfect balance and randomization guarantees it by construction, because it provides orthogonality of the treatment to the other \(P\) causes represented in our causal model. In other words, we know nothing was used in determining treatment assignments except a coin flip.
Still, there are threats to the internal validity of the experiments, which can undermine our causal inference. First, violation of SUTVA whereby subjects in the two groups interact with each other can happen in many social and economic applications. If that happens the comparisons we make would no longer between treated and control, but between treated and partially treated.
Second, ruling out confounding due to common causes is guaranteed in expectation, which means the probability that treatment and control only differ in treatment assignment and nothing else gets arbitrarily higher as the sample size increases. In a given sample, especially if it is small, the net effects of other causes might not be zero, and this can bias the ATE.
As such, it is always good practice to examine the balances in observables between treated and control in our sample before analyzing the experiment. Typically this is done by computing the normalized differences as a scale-free measure of the difference in distributions instead of the t-statistic. Specifically, for each covariate, we report the difference in averages by treatment status, scaled by the square root of the sum of the variances:
\[ \Delta_X = \frac{\bar{X_1}-\bar{X_0}}{\sqrt{S_1^2 + S_0^2}} \] where \(S_1^², S_0^²\) is the sample variance of the treated and control, respectively. As a rule of thumb, differences larger than 0.10, might indicate imbalance, which would call for covariate adjustment in the analysis. Notice, however, we have no way to test whether common unobservable causes are eliminated in our experiment. We simply assume if balance is achieved in observables it is plausible that it will hold in unobservables as well. But, this might not be the case, especially in small samples.
We also need to be mindful about the generalizability of experiment findings, i.e. their external validity. It is important to recognize that experiments allow us to identify the treatment effect within the population used in the study. Also, unless the experiment is designed for measuring long-term effects, the estimated ATE usually applies for the short-term. It is common to treat the estimates from an experiment as if it were the truth, not just in the study sample but more generally, but this might not be valid.
There are many cases where businesses decided to scale operations based on experiment findings in one market, sample or time period, and failed because those findings had not been proven to be generalizable. In general, to ensure valid extrapolation, we either need random sampling in addition to randomization of treatment or additional assumptions. For example, if we have an online experiment, to ensure that findings are generalizable to all users within a predetermined location, we need to eliminate day of the week and time of the day effects by sampling visitors randomly throughout the day as well as the week.
Conclusion
Causal inference is difficult due to its inherent uncertainty, and progress can be made so long we improve our understanding of the most critical part: identification. Randomized experiments require fewer identifying assumptions than any other identification strategy. What is more, these assumptions are much more plausible in experiments. These two traits together have earned experiments the gold standard status in causal inference. Nevertheless, experiments can still lack internal validity if they are not conducted properly, and generalizing experiment findings is challenging in its own ways.
References
[1] L. Keele, The Statistics of Causal Inference: A View from Political Methodology. (2015), Political Analysis.
[2] A. Lewbel, The Identification Zoo-Meanings of Identification in Econometrics. (2019), Journal of Economic Literature.
[3] G. W. Imbens and J. M. Wooldridge, Recent Developments in the Econometrics of Program Evaluation, (2009), Journal of Economic Literature.
[4] J. List, The Voltage Effect: How to Make Good Ideas Great and Great Ideas Scale, (2022).
- Posted on:
- March 6, 2023
- Length:
- 7 minute read, 1467 words
- Categories:
- Causal Inference
- Tags:
- Causal Inference